[오일러 프로젝트] 131번 - 세제곱수와 소수의 관계
오일러 프로젝트 - 131번 문제
문제
어떤 소수 p는 n3 + n2p를 세제곱수로 만드는 자연수 n이 존재합니다.
예를 들어 p = 19라면, 83 + 82×19 = 123 입니다.
매우 놀라운 사실은 이런 특성을 가진 소수마다 n이 단 한개만 존재한다는 점입니다. 100 이하에 이런 소수는 정확히 4개 존재합니다.
이런 놀라운 특성을 가진 소수가 백만 이하에 몇 개나 있습니까?
풀이
이 문제는 코드화해서 생각해보면 나누어보면 2가지 측면이 있습니다.
어떤 소수 p n3 + n2p = m3를 만족하는 p
첫 풀이인 만큼 시간복잡도는 생각하지 않고 만들겠습니다. 참고로 사용 언어는 자료형, 컴파일의 귀찮음을 방지하기 위해 Chrome 개발자 도구에서 js로 풀이할 예정입니다
소수를 판별할 때 사용할 함수
소수를 찾는 데는 가장 쉬운 방법인 에라토스 테네스 체를 사용하겠습니다.
function isPrime(num) {
let result = true
for (var i = 2; i <= Math.sqrt(num); i++) {
if (num % i === 0) {
result = false
}
}
return result
}
식에 부합하는지 확인할 함수
function check(p,m) {
let result = false
if((n**3) + (n**2 * 2) === m**3) {
result = true
}
return result
}
참고로 js에선 내장객체인 Math 객체의 cbrt 메서드로 세제곱근을 확인할 수 있습니다.
Math.cbrt(125) // 5
여기까지만 보면 참 쉽습니다
그냥 처음부터 하나씩 넣어보고 결정하면 되는거 아닌가?
맞습니다. 그렇게 생각하면 참 간단한 문제입니다. 이를 기반으로 일단 100이하의 소수까지만 한번 코드를 짜보겠습니다. n과 m의 최댓값을 임시로
//소수인지 체크하는 부분
function isPrime(num) {
let result = true
for (let i = 2; i <= Math.sqrt(num); i++) {
if (num % i === 0) {
result = false
}
}
return result
}
//소수를 찾아서 primes 배열을 생성하는 부분
let primes = [];
for (let i = 2; i < 100; i++) {
if (isPrime(i)) {
primes.push(i)
}
}
console.log(primes);
//생성된 primes 배열을 바탕으로 계산하는 부분
let cnt = 0;
let results = [];
for (cnt = 0; cnt < primes.length; cnt++) {
let p = primes[cnt];
for(let n = 1; n < 5000; n++) {
for(let m = 1; m < 5000; m++) {
if(n**3 + n**2 * p === m ** 3) {
results.push({p:p, n:n, m:m})
continue;
}
}
}
}
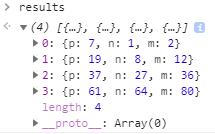
console.log(results);
결과는 다음과 같습니다.
표본이 적은거 같으니 좀 더 뽑아보겠습니다.
이렇게 컴퓨터를 혹사시킨다면 1,000,000 이하의 소수를 모두 찾을 수는 있겠죠. 하지만 우리는 이런걸 원하는게 아니죠? 숫자 사이의 상관관계를 찾아보겠습니다.
먼저 p. p는 소수입니다. 이 이외의 딱히 규정지을만한 규칙은 보이지 않는군요.
둘째로 n. 식에서 n을 세제곱, 제곱하여 계산하는데 놀랍게도 n은 그 자체만으로 이미 세제곱수 입니다. 1, 8, 27, 64, 216… 모두 1, 2, 3, 4, 6의 세제곱수이죠. 증가되는 규칙이 있나 살펴봤지만 딱히 있는것 같지는 않군요
셋째로 m입니다. 원가 규칙이 있는 듯 하면서도 안보이는군요. 사실 여기서 꽤 해맸습니다. 소인수분해도 해보고 나눠도 보고 곱해도 보고.. 한 1~2시간 고민하다가 n/m을 생각하게 되었죠.
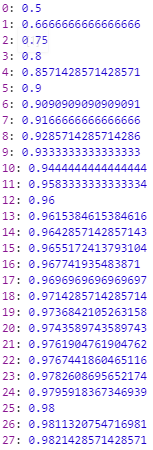
처음에는 막연히 증가되는 규칙이 있을거라 생각하고 쭉 결과값들을 써봤습니다.
아! 1에 점점 수렴하는군요! 이 수렴하는 값에 규칙이 있을줄 알았는데, 소수점 계산이 정확하지 않은 js의 특성도 있고, 어차피 여기서 규칙을 찾기는 힘들거같아 다른 규칙을 생각해봤습니다.
n/m은 순환소수구나!
순환소수는 어느정도 아실거라 생각합니다. 순환소수라는 것은 정수/정수 꼴로 표현할 수 있다는 것을 뜻하고, 이를 표현하면
1/2 (=> n=1, m=2)
2/3 (=> n=8, m=12)
3/4 (=> n=27, m=36)
4/5 (=> n=64, m=80)
6/7 (=> n=216, m=252)
9/10 (=> n=729, m=810)
10/11 (=> n=1000, m=1100)
11/12 (=> n=1331, n=1452)
...
와! 전부다 (k-1)/k 꼴이네요. n/m이 1에 수렴하는 이유가 여기에 있었군요. 그래서 문제의 제목도 소수와 세제곱수의 협력관계인가 봅니다.
근데 한가지 문제가 있죠. 5/6, 7/8, 8/9같은 친구들은 왜 빠져있을까요? 일단 식을 세워서 위의 친구들을 n^3 + n^2p = m^3의 꼴로 만들어보겠습니다.
규칙을 찾아보니 a / b 꼴에 a^2가 분자와 분모에 곱해진 꼴이군요. 식을 p를 기준으로 정리해서 p값을 구해보겠습니다.
n = a * a**2
m = (a+1) * a**2
p = (m**3 - n**3) / (n**2)
식이 정말 간단해졌네요 식에서 a=5라고 잡으면 왜 5/6이 포함이 안되는지 알 수 있겠죠? 대입해서 계산해보면 p는 91이 나옵니다. 아! 91은 소수가 아니니 포함되지 않은거였군요.(7*13 = 91)
자! 그러면 계산은 더욱 간단해졌습니다. 구한 소수를 바탕으로 1/2, 2/3, 3/4, 4/5… 쭉쭉 p가 소수가 나오는지만 확인하고, 백만까지 몇개의 소수가 포함되는지 확인하면 되겠네요
최종 코드를 짜봅시다!
function isPrime(num) {
let result = true
for (var i = 2; i <= num-1; i++) {
if (num % i === 0) {
result = false
}
}
return result
}
let results = [];
for(a = 0; ; a++) {
m = (a+1) * (a)**2
n = (a) * (a)**2
p = ( m**3 - n**3 ) / ( n**2 )
//결과값 p가 1,000,000이 넘으면 break;
if(p > 1000000) break;
//결과값 p가 정수가 아니면 continue
if(p % 1 !== 0) continue;
//결과값 p가 소수인지 확인
if (isPrime(p)) {
results.push({p:p, n:n, m:m, a: a})
}
}
console.log(results);
근데 문제가 생겼습니다… 위 식을 크롬 개발자 도구든 nodejs든 아무리 계산을 해도 정답은 48이 나오는데… 자꾸 틀렸다네요..? 논리적인 방법을 통해 나온 규칙이고, 자만일수도 있지만 분명 틀린게 없다고 생각했는데 ㅜㅜ 그러다 JS의 특징이 하나 생각났습니다.
p = ( m**3 - n**3 ) / ( n**2 )
지난번에도 오일러 프로젝트 문제를 풀던 중, 분명 맞는 식이고 괜찮은 것 같은데 답이 달라서 여러 방법을 찾던 중이었습니다. 당시에는 파이썬도 함께 연습하던 참이라 파이썬으로 번역한 코드도 실행시켜 봤는데, 이럴수가… 두 코드의 답이 달랐습니다. 언어의 차이가 있겠지만 분명 같은 알고리즘에 코드간 번역을 제외하면 완전히 같은 코드인데, 왜 답이 달랐을까요?
JS가 JS 했다.
말 그대로입니다…
https://stackoverflow.com/questions/3439040/why-does-adding-two-decimals-in-javascript-produce-a-wrong-result
js 유저라면 한번쯤 겪어봤을 문제.
0.1 + 0.2는 0.3000000000000004가 되는 놀라운 기적.
결국 Math.round()를 써서 소수 부분을 없애기로 했습니다. 혹여나 알고리즘에 이상이 생길까 했지만, 어차피 round를 해줘도 소수인지 아닌지는 판별이 가능하기 때문에 크게 상관 없을 것 같았죠…
진짜 최종 코드
function isPrime(num) {
let result = true
for (var i = 2; i <= num-1; i++) {
if (num % i === 0) {
result = false
}
}
return result
}
let results = [];
for(a = 0; ; a++) {
m = (a+1) * (a)**2
n = (a) * (a)**2
p = Math.round(( m**3 - n**3 ) / ( n**2 ))
//결과값 p가 1,000,000이 넘으면 break;
if(p > 1000000) break;
//결과값 p가 정수가 아니면 continue
if(p % 1 !== 0) continue;
//결과값 p가 소수인지 확인
if (isPrime(p)) {
results.push({p:p, n:n, m:m, a: a})
}
}
console.log(results);
이리하여 나온 정답은 173. 그렇게 131번 문제의 첫번째 풀이자가 되었습니다 야호!